Применения аддитивной теории чисел
Аддитивной теорией чисел называется раздел математики, в котором изучается, какие числа можно представить в виде суммы некоторого множества заданных чисел. Долгое время считалось, что это — исключительно теоретическая часть математики. Но оказывается, что есть задачи практического характера, которые решаются с помощью этой теории. Например, некоторые транспортные задачи логистики.
В логистике имеется много задач, связанных с транспортными перевозками. Эти траспортные задачи очень разнообразны. Вот одна из таких задач; в ней предполагается, что имеется два типа транспортных средств, которые могут вмещать некоторое целое количество, например, партий груза или целое количество людей.
Приведу конкретный пример.
Транспортная компания, специализирующаяся на перевозках автомобилей с завода к авторизованным дилерам, использует малые и большие автовозы с вместимостью три и шесть автомобилей соответственно.
Стоимость использования этих автовозов для компании составляет 80 и 100 тысяч рублей соответственно. За каждый перевезенный автомобиль компания получает от дилера 20 тысяч рублей. Один автомобиль компания перевозит бесплатно в качестве бонуса. Если компания считает заказ на перевозку выгодным, когда прибыль составляет не менее 60 тысяч рублей, то сколько автомобилей могут быть перевезены, чтобы эта цель была достигнута?
Составим модель ситуации. Пусть x — количество малых автовозов, y — количество больших автовозов, n — количество оплачиваемых перевозимых автомобилей. Число n не может быть больше, чем 3x + 6y − 1. Доход от выполненного заказа составит 20n тысяч рублей, но(80x + 100y) тысяч рублей уйдут в расходы. И еще надо учесть желательную прибыль. Транспортный заказ будет прибыльным, если найдутся такие неотрицательные целые числа x и y, что
⎧⎨⎩
20n≥80x + 100y + 60
n≤3x + 6y − 1
Упрощая первое неравенство, получим равносильную систему неравенств
⎧⎨⎩
n≥4x + 5y + 3
n≤3x + 6y − 1
Множество таких неотрицательных целых чисел n, для которых эта система имеет решение, и дает ответ на поставленный вопрос.
В общем случае задача математически ставится так. Найти множество всех таких неотрицательных целых чисел n, что двойное неравенство
ax + by + c≤n≤dx + ey − f
верно для некоторых неотрицательных целых x и y.
Числа a, b, d, e, c, f — это параметры задачи. Они будут различаться от одной задачи к другой. Числа x, y, n — это неизвестные, которые могут быть определены при решении неравенств. Но если величины x, y (а это количества автовозов разных типов) нужны для непосредственной организации перевозки, то величину n нужно определить в первую очередь для того, чтобы понять, выгоден заказ компании или нет.
Будем обозначать поставленную общую задачу P(a, b;d, e;c, f), тогда P(4, 5;3, 6;3, 1) — это частная задача, рассмотренная в виде примера.
Вот еще один пример.
Туристическое агентство, специализирующееся на организации туристических экскурсий по городу, использует малые и большие автобусы. В малом автобусе 30 мест для пассажиров, в большом — 50 мест. Аренда малого автобуса стоит 15500 рублей, большого автобуса — 24 тысяч рублей. Цена экскурсии для одного человека составляет 500 рублей, но бесплатна для руководителя туристической группы.
Задача заключается в следующем. Если группа из n человек (и одного руководителя) заказывает экскурсию, получит ли агентство прибыль?
Составим модель ситуации. Пусть x — количество малых автобусов, y — количество больших автобусов. Тогда размер группы (включая руководителя), т.е. число n + 1 не может быть больше, чем 30x + 50y. Доход агентства составит 500n рублей, но потребуются расходы, равные(15, 5x + 24y) тысяч рублей. Заказ на экскурсию будет прибыльным, если найдутся такие неотрицательные целые числа x и y, что
⎧⎨⎩
0, 5n > 15, 5x + 24y
n + 1≤30x + 50y
Упрощая первое неравенство, получим равносильную систему неравенств
⎧⎨⎩
n > 31x + 48y
n + 1≤30x + 50y
Чтобы задача имела такой же вид, как и предыдущая, установим минимальную прибыль в 1000 рублей. Тогда задача сводится к тому, чтобы найти множество всех таких неотрицательных целых чисел n, для которых имеет решение двойное неравенство
31x + 48y + 2≤n≤30x + 50y − 1
Ясно, что эта задача может быть записана как P(31, 48;30, 50;2, 1).
Прежде чем решать эти задачи, рассмотрим несколько более простые задачи, в которых ситуация описывается вместо неравенств уравнениями.
Задача о почтовых марках. Имеется большой запас 5- и 8-рублевых марок. Можно ли ими в точности оплатить 27-рублевую открытку?
На язык алгебры задача переводится так. Существует ли решение уравнения
5x + 8y = 27
где x = число 5-рублевых марок, y = число 8-рублевых марок.
Эта задача не имеет большого практического значения, но интересна в математическом плане. Уравнения такого вида, как записанное выше, называются диофантовыми уравнениями, в честь древнегреческого математика Диофанта Александрийского, написавшего дошедшую до наших дней книгу «Арифметика». Диофантовы уравнения — это уравнения с целыми коэффициентами, решения которых требуется найти среди целых чисел. Но вернемся к нашему уравнению.
Легко определить, есть ли решение, когда неизвестное в уравнение одно. Но в уравнении два неизвестных, поэтому надо испробовать различные варианты, подставляя вместо x = 0, 1, 2, 3 и так далее. Можно попробовать и убедиться, что не получается найти решение в целых неотрицательных числах. Если бы разрешались целые отрицательные числа, то решение в конце концов нашлось бы: x = 7, y = − 1. Но в том-то и дело, что марок не может быть отрицательное количество.
Поэтому постараемся определить, какие числа n могут быть получены путем сложения некоторого количества пятерок и некоторого количества восьмерок. Это – числа, для которых верно
n = 5x + 8y
где x и y — целые неотрицательные числа. Множество всех таких n можно вычислить, это
S = {0 ,5,8,10,13,15,16,18,20,21,23,24,25,26,28, → }.
Стрелка означает, что все числа, следующие за 28, тоже принадлежат данному множеству.
0 = 5⋅0 + 8⋅0, 5 = 5⋅1 + 8⋅0, 8 = 5⋅0 + 8⋅1, 10 = 5⋅2 + 8⋅0,
13 = 5⋅1 + 8⋅1, 15 = 5⋅3 + 8⋅0, 16 = 5⋅0 + 8⋅2, 18 = 5⋅2 + 8⋅1,
и т.д. С другой стороны, есть числа, которые не могут быть получены сложением пятерок и восьмерок. Они образуют множество
G = {1, 2, 3, 4, 6, 7, 9, 11, 12, 14, 17, 19, 22, 27}.
Множество S называется числовой полугруппой с генераторами 5 и 8, и обозначается S = ⟨5, 8⟩, а G называется множеством пробелов полугруппы S. Число 28 в полугруппе S, которое стоит перед стрелкой, называется кондуктором полугруппы S. Название «кондуктор» объясняется тем, что он как бы ведет за собой все последующие числа. Так что все числа, начиная с 28, могут быть получены сложением пятерок и восьмерок. Напротив, число 27 — это последнее число, которое нельзя получить, складывая пятерки и восьмерки.
Английский математик XIX века Джеймс Сильвестр исследовал общую задачу о почтовых марках, которая формулируется так. Пусть даны два целых положительных числа a и b. Какие числа можно получить сложением этих двух чисел, взятых в произвольных количествах, т.е. для каких чисел верно
n = ax + by
где x и y — целые неотрицательные числа?
Оказывается, есть несложная формула для кондуктора числовой полугруппы S = ⟨a, b⟩ с генераторами a и b. Кондуктор c равен
c = (a − 1)(b − 1).
Число пробелов полугруппы S = ⟨a, b⟩ в два раза меньше кондуктора:
g = (c)/(2) = ((a − 1)(b − 1))/(2).
Это можно проверить на примере S = ⟨5, 8⟩. Действительно,
c = (5 − 1)⋅(8 − 1) = 28, g = (28)/(2) = 14.
* * *
На некоторое время забудем, что рассматриваемые числа неотрицательные, и будем считать их просто целыми. Тогда уместно будет вспомнить соотношение Безу (названное в честь французского математика XVIII века Этьена Безу): для целых чисел a и b, хотя бы одно из которых не нуль, существуют такие целые числа x и y, что выполняется соотношение:
НОД(a, b) = x⋅a + y⋅b.
где НОД — наибольший общий делитель.
Это значит, что диофантово уравнение
n = ax + by,
решаемое в целых числах, не только неотрицательных, но и отрицательных, имеет решения при любых n, кратных НОД(a, b), и ни при каких других. Например,
1 = 5x + 8y
верно при x = − 3, y = 2. Поэтому, если допускать, чтобы x и y принимали любые целые значения, уравнение
n = 5x + 8y
всегда разрешимо.
* * *
Но, поскольку нас интересует задача из реальной жизни, вернемся к неотрицательным числам. Заметим, что если НОД(a, b) не равен единице, то кондуктор может не существовать. Например,
⟨6 ,8⟩ = {0, 6, 8, 12, 14, 16, 18, 20, ...},
и, начиная с 12, множество содержит все следующие четные числа, но не содержит нечетных, так как НОД(6, 8) = 2. Так что для того, чтобы множество S = ⟨a, b⟩ с генераторами a и b было числовой полугруппой и имело кондуктор, надо потребовать, чтобы a и b были взаимно простыми числами, т.е. НОД(a, b) = 1.
Исследуем подробнее, какие числа n представимы в виде суммы пятерок и восьмерок, т.е.
n = 5x + 8y
где x и y — целые неотрицательные числа. Составим таблицу представления чисел, скажем, до 40.

Такую таблицу составить нелегко. Каждый раз требуется подбирать множители для пятерки и восьмерки. Но можно заметить, что это, в сущности, таблица сложения для чисел, кратных 5, и чисел, кратных 8. В чистом виде такая таблица будет выглядеть так:
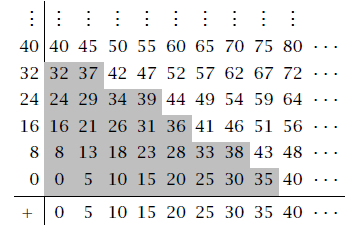
Серым цветом выделены те числа, которые были представлены в предыдущей таблице. Если ограничить таблицу первыми пятью строками и первыми восемью столбцами, и из каждого числа, стоящего выше ступенек, вычесть 40, то получим:
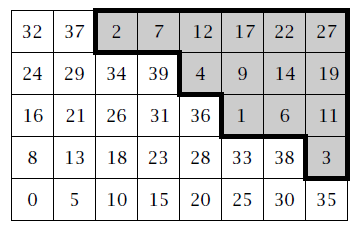
Здесь выделены непредставимые числа, т.е. пробелы полугруппы, которые, как мы знаем, образуют множество
G = {1, 2, 3, 4, 6, 7, 9, 11, 12, 14, 17, 19, 22, 27}.
Таблицу чисел, представимых в виде суммы пятерок и восьмерок, можно записать иначе. Будем записывать все целые неотрицательные числа подряд, по пять чисел в строке:
| 0 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 32 | 33 | 34 |
Тогда выше зигзагообразной линии находятся все непредставимые числа.
* * *
Есть еще одна задача, являющаяся естественным усложнением задачи о почтовых марках.
Задача о Мак-Наггетсах. В МакДональдсе продаются Чикен Мак-Наггетсы в коробках по 6, 9 и 20 штук. Чему равно наибольшее количество Мак-Наггетсов, которые нельзя заказать?
С алгебраической точки зрения, в задаче требуется найти наибольшее положительное целое число n такое, что уравнение
n = 6x + 9y + 20z
не имеет решений. Переменные x, y и z предполагаются неотрицательными целыми. Ответом является число 43, что можно увидеть из таблицы:
| 0 | 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 32 | 33 | 34 | 35 |
| 36 | 37 | 38 | 39 | 40 | 41 |
| 42 | 43 | 44 | 45 | 46 | 47 |
| 48 | 49 | 50 | 51 | 52 | 53 |
* * *
Литература
1. Michael T. S. How to Guard an Art Gallery And Other Discrete Mathematical Adventures. — Baltimore: The Johns Hopkins University Press, 2009. — xi, 257 pp. (Chapter 6, p. 169–205).
2. Coin problem. //en.wikipedia.org/wiki/Coin_problem.
3. Robles-Pérez A.M. and Rosales J.C. Numerical semigroups in a problem about cost-effective transport. Forum Math. 29(2) (2017), 329–345.
4. Robles-Pérez A.M. and Rosales J.C. On a transport problem and monoids of non-negative integers. //arxiv.org/abs/1611.02627.